รูปที่ทำจากกระดาษอาจจะแตกต่างกันได้- อย่างไรก็ตาม ส่วนใหญ่มักจะให้ความสำคัญกับรูปทรงเรขาคณิต สิ่งหนึ่งคือรูปทรงยี่สิบหน้า (รูปแบบการติดกาว) ซึ่งเรียกได้ว่าทั้งซับซ้อนและเรียบง่ายในเวลาเดียวกัน ซับซ้อนเพราะมีหลายหน้า – 20 ชิ้น และมีขอบมากถึง 30 ชิ้น ง่ายๆ เพราะมันสมมาตรตรงจุดศูนย์กลางอย่างสมบูรณ์แบบ
คำอธิบายรูปภาพ
รูปทรงยี่สิบหน้า (รูปแบบการติดกาวจะแสดงไว้ในบทความด้านล่าง) เป็นรูปที่ได้รับชื่อเมื่อประมาณ 100 ปีที่แล้ว มาจากตัวเลขกรีกโบราณ “ikosi” ซึ่งแปลว่า “20” ส่วนอีกส่วนหนึ่งของชื่อมาจากคำว่า "เฮดรา" ซึ่งแปลว่า "ขอบ" ปรากฏว่าชื่อดังกล่าวสามารถแปลจากภาษากรีกได้ว่า "20 ด้าน"
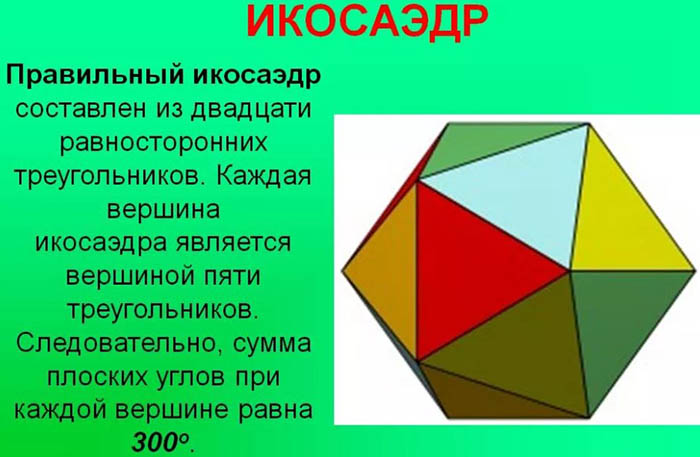
เพื่อให้วัตถุทางเรขาคณิตสามมิติถูกเรียกว่าทรงยี่สิบหน้าปกติ จะต้องเป็นไปตามเงื่อนไขต่อไปนี้:
- ต้องมีหน้าจำนวน 20 หน้าพอดี (ไม่มากกว่าหรือน้อยกว่านี้)
- แต่ละหน้าจะต้องเป็นรูปสามเหลี่ยมด้านเท่า ในเรขาคณิต สามเหลี่ยมจะถูกเรียกว่ารูปปกติ ถ้ามุมทั้งหมดเท่ากัน มุมแต่ละมุมของสามเหลี่ยมนี้มีค่าเท่ากับ 60 องศา
รูปทรงยี่สิบหน้า (icosahedron) คือ รูปทรงหลายหน้าปกติ และเป็นหนึ่งในรูปทรงห้าเหลี่ยมที่เรียกว่า “รูปทรงเพลโต”
ลักษณะเด่นอื่นๆ มีดังนี้:
- จำนวนด้านของแต่ละหน้าทั้ง 20 หน้าคือ 3 ด้าน
- จำนวนจุดยอด (จุดเชื่อมต่อด้านข้างของหน้า) – 12;
- จำนวนของขอบ (ด้านของหน้า) ที่บรรจบกันที่จุดยอด (จุด) แต่ละจุดคือ 5
- จำนวนซี่โครงทั้งหมด – 30;
- จำนวนแกนสมมาตร - 15;
- จำนวนระนาบสมมาตร – 15

อย่างไรก็ตาม ลักษณะเฉพาะทั้งหมดเหล่านี้สืบเนื่องมาจากสองลักษณะหลักที่กล่าวไว้ข้างต้น หากรูปทรงหนึ่งมี 20 หน้า และแต่ละหน้าเป็นรูปสามเหลี่ยมด้านเท่า ดังนั้นรูปทรงนั้นจะเป็นรูปยี่สิบหน้าปกติพร้อมคุณสมบัติทั้งหมด
ทรงยี่สิบหน้า (รูปแบบการติดกาวนั้นไม่ยากแม้แต่สำหรับผู้เริ่มต้น) เป็นรูปที่มีพื้นที่กำหนดได้ง่าย แม้ว่าจะมีหน้าจำนวนมากก็ตาม นอกจากนี้ ยังสามารถแสดงเป็นพื้นที่กวาดได้อีกด้วย ถ้าทราบพื้นที่ของรูปสามเหลี่ยม 1 ใน 20 รูปที่เป็นหน้าของรูปนั้นแล้ว การคูณตัวเลขนี้ด้วย 20 ก็เพียงพอแล้ว
เช่น หากพื้นที่ของสามเหลี่ยมแต่ละอันคือ 4 ตารางเซนติเมตร ดังนั้น พื้นที่ทั้งหมดของพื้นผิวของรูปทรงยี่สิบหน้าจะเท่ากับ 80 ตารางเมตร การจะทำเช่นนี้ จะต้องคูณ 4 ด้วย 20
ประเภทหลัก
รูปทรงยี่สิบหน้าที่ทำจากกระดาษอาจจะแตกต่างกันได้
เช่น หาก:
- ถ้าหากคุณใช้กระดาษสีเดียวในการทำงาน รูปก็จะกลายเป็นสีเดียว
- มันจะเป็นกระดาษสี คุณสามารถทำรูปทรงยี่สิบหน้าหลากสี ซึ่งจะเล่นกับสีต่างๆ และดูสวยงามมากขึ้น
มักทำเป็นรูปยี่สิบหน้าซึ่งมีลักษณะเหมือนลูกฟุตบอลโดยมีรูปสามเหลี่ยมสีขาวสลับกับรูปสามเหลี่ยมสีดำ ในความเป็นจริงแล้วมันจะไม่ใช่ลูกบอล เนื่องจากมันไม่กลมเลย สิ่งที่ทำได้ยากกว่าคือรูปทรงยี่สิบหน้าซึ่งมีรูปร่างเหมือนดวงดาว มีแง่มุมบางอย่างที่นี่ที่โดดเด่นเมื่อเทียบกับพื้นหลังของแง่มุมอื่นๆ
รูปทรงที่สวยงามที่สุดคือทรงยี่สิบหน้าซึ่งประดับประดาด้วยองค์ประกอบการตกแต่งต่างๆ สิ่งเหล่านี้อาจเป็นของตกแต่งอะไรก็ได้: ของที่เป็นมันวาว สว่างสดใส หรือของที่สามารถติดบนพื้นผิวกระดาษได้อย่างง่ายดาย ทรงยี่สิบหน้าทรงนี้สามารถใช้เป็นของเล่นปีใหม่และแขวนบนต้นคริสต์มาสได้

ในเรขาคณิตมีรูปทรงหลายเหลี่ยมนับไม่ถ้วน บางอันมีความสมมาตรมากกว่า ในขณะที่บางอันกลับมีความสมมาตรน้อยกว่า รูปทรงที่พบมากที่สุดคือทรงยี่สิบหน้าปกติ ซึ่งมีหน้าเหมือนกันทุกประการ 20 หน้า ในทางคณิตศาสตร์ ทรงยี่สิบหน้าปกติสามารถเรียกได้ว่าเป็นวัตถุนูนหรือไม่นูนก็ได้
ทั้งนี้ แต่ละอันมีหน้า 20 หน้าและมีขอบมากกว่า 1.5 เท่า ทั้งสองมีสิ่งที่เรียกว่าสมมาตรทรงเก้าหน้า อย่างไรก็ตาม รูปแบบนูนมักจะถูกเรียกว่ารูปทรงยี่สิบหน้าปกติ ในขณะที่รูปแบบไม่นูนจะจัดอยู่ในประเภทของรูปทรงยี่สิบหน้าใหญ่
รูปทรงยี่สิบหน้า (สแกนเพื่อติดกาว) สามารถแสดงได้ด้วยตัวเลือกต่อไปนี้:
| รูป | คำอธิบาย |
| ทรงยี่สิบหน้านูน | มี 20 หน้าและจุดยอด 12 จุด ทรงตันทางเรขาคณิตนี้มีรูปทรงหลายเหลี่ยมสองรูป เรียกว่า โดเดคาฮีดรอนปกติ มีหน้าปกติ 5 ด้านจำนวน 3 หน้าล้อมรอบจุดยอดแต่ละจุด |
| ทรงยี่สิบหน้าขนาดใหญ่ | มีหน้าทั้งหมด 20 หน้า โดยแต่ละหน้าเป็นรูปสามเหลี่ยมด้านเท่า อย่างไรก็ตาม จุดยอดของมันไม่ใช่รูป 5 เหลี่ยม แต่เป็นรูปดาวห้าแฉก นั่นคือเหตุผลที่ขอบจึงตัดกันทางเรขาคณิต เมื่อตัดกันจะไม่เกิดขอบใหม่เกิดขึ้น ทรงหลายหน้าคู่ของทรงยี่สิบหน้าใหญ่คือทรงสิบสองหน้าใหญ่ มี 3 หน้ารวมกันอยู่รอบจุดยอดแต่ละจุด โดยแต่ละหน้าเป็นรูป 5 เหลี่ยม |
| รูปหลายเหลี่ยมคล้ายรูปดาว | หากหน้าหรือขอบของรูปทรงหลายเหลี่ยมขยายออก เมื่อสัมผัสกัน จะเกิดรูปดาวขึ้น สิ่งนี้เกิดขึ้นแบบสมมาตร ดังนั้นวัตถุที่ได้จึงมีสมมาตรเหมือนกับรูปร่างเดิม ผลงานทางวิทยาศาสตร์ของ Coxeter ที่มีชื่อว่า "59 icosahedra" ระบุรายชื่อรูปทรงหลายเหลี่ยมแบบมีดาวเกือบ 60 แบบ หลายอันมีด้านแยกกันในแต่ละระนาบทั้ง 20 ระนาบ ร่างกายอื่นๆ อีกมากมายมีมากกว่า 1 ใบหน้าบนเครื่องบิน สามารถสร้างได้โดยการรวมรูปทรงหลายเหลี่ยมที่เรียบง่ายเข้าด้วยกัน |
| ซูโดอิโคซาฮีดรอน | รูปร่างทรงยี่สิบหน้าที่บิดเบี้ยวปกติ ทำให้ความสมมาตรลดลง |
| ทรงยี่สิบหน้าของเจสเซน | หากวัตถุทางเรขาคณิตสามมิติมีหน้า 12 หน้า โดยแต่ละหน้าเป็นสามเหลี่ยมหน้าจั่ว และหน้าเหล่านี้ถูกจัดเรียงในลักษณะที่ทำให้กลายเป็นวัตถุที่ไม่นูน ดังนั้น รูปร่างนี้จะถูกเรียกว่า icosahedron ของ Jessen (หรือ icosahedron ตั้งฉากกัน) แล้ว มันมีมุมฉากสองด้าน ลักษณะเด่นประการหนึ่งคือสามารถแยกส่วนเท่าๆ กันด้วยรูปหกเหลี่ยมซึ่งแต่ละหน้าเป็นรูปสี่เหลี่ยมจัตุรัส ซึ่งหมายความว่ามันสามารถแบ่งออกเป็นหลายเหลี่ยมเล็ก ๆ แล้วนำมาใช้สร้างรูปหกเหลี่ยมที่มีหน้าเท่ากันได้ รูปหกเหลี่ยมนี้คือลูกบาศก์ |
วิธีการทำรูปทรงยี่สิบหน้าปกติจากกระดาษ?
การพัฒนาการติดกาว Icosahedron เพื่อการผลิตจะต้องเตรียมวัสดุและเครื่องมือดังต่อไปนี้:
- กระดาษ. อาจจะเป็นกระดาษลูกฟูก สีขาว หรือสีก็ได้ ความหนาแน่นของมันยังสามารถแตกต่างกันได้
- กรรไกร. จำเป็นสำหรับการตัดรูปร่างและขนาดตามต้องการ
- กาว. ตัวเลือกที่ดีที่สุดคือ PVA ทั่วไป เพราะใช้เวลาในการแห้งนาน ซึ่งเพียงพอที่จะขจัดข้อผิดพลาดที่อาจเกิดขึ้นได้
- ไม้บรรทัด. ถ้าไม่มีสิ่งนี้ การจะพับกระดาษให้โค้งเท่าๆ กันตามแนวพับก็จะยากมาก

คุณยังสามารถใช้วัสดุเพิ่มเติมเพื่อตกแต่งงานกระดาษของคุณได้ มันเป็นเรื่องของรสนิยมและจินตนาการ
หลังจากเตรียมวัสดุและเครื่องมือทั้งหมดแล้ว คุณสามารถดำเนินการสู่กระบวนการสร้างสรรค์ได้โดยตรง
การทำงานจะเกิดขึ้นในขั้นตอนต่อไปนี้:
- พิมพ์เทมเพลตที่เสร็จแล้วบนเครื่องพิมพ์ และถ่ายโอนไปยังวัตถุดิบที่เตรียมไว้ ต้องระมัดระวังในการถ่ายโอน มิฉะนั้นการทำเครื่องหมายจะไม่ถูกต้องซึ่งหมายความว่ารูปร่างโดยรวมจะออกมาไม่เท่ากันหรือไม่มีเลย ขอแนะนำให้ใช้ไม้บรรทัดเป็นอย่างยิ่ง
- เริ่มตัดแม่แบบออกมา กรรไกรจะต้องตัดตามเส้นประอย่างเคร่งครัด มิฉะนั้น จะไม่สามารถติดกาวส่วนประกอบทั้งหมดของรูปเข้าด้วยกันได้ อย่างไรก็ตาม คุณไม่ควรเร่งรีบ เพราะเทมเพลตอาจเสียหายได้ง่ายจากการเคลื่อนไหวที่ไม่ระมัดระวัง สิ่งสำคัญคือองค์ประกอบสามเหลี่ยมทั้งหมดของเทมเพลตจะต้องมีด้านเท่ากัน นี่คือคุณสมบัติหลักประการหนึ่งของรูปทรงยี่สิบหน้า มันมีความสำคัญและจำเป็นต้องมีเช่นเดียวกับเงื่อนไขที่ว่าด้านทั้งหมดของสี่เหลี่ยมจัตุรัสเดียวกันจะต้องเท่ากันเสมอ หากฝ่าฝืนกฎนี้ ความแตกต่างระหว่างทั้งสองฝ่ายจะเห็นได้ชัดมาก
- หลังจากตัดส่วนว่างออกแล้ว ให้เริ่มดัดรูปร่าง ที่นี่ต้องใช้ไม้บรรทัดแน่นอน จุดพับจะแสดงเป็นเส้นทึบ และควรติดกาวตามเส้นประ เป้าหมายหลักคือการเชื่อมต่อทุกด้านขององค์ประกอบสามเหลี่ยมของรูปร่างอย่างถูกต้อง หากด้วยเหตุผลบางประการคุณไม่มีกาว PVA ในมือ และคุณพบกาวแห้งเร็วแทน คุณควรจำไว้ว่าไม่มีที่ว่างสำหรับข้อผิดพลาด หากคุณเชื่อมต่อชิ้นส่วนไม่ถูกต้องและกาวแห้งภายในไม่กี่วินาที ก็จะไม่สามารถแยกองค์ประกอบต่างๆ ออกได้อีกต่อไป หากคุณใช้กาว PVA คุณจะต้องกดข้อต่อแต่ละจุดให้แน่น หลังจากทากาวแล้ว ให้กดชิ้นส่วนทั้งสองชิดกันประมาณ 20 วินาที
- ตกแต่งผลิตภัณฑ์สำเร็จรูป สำหรับสิ่งนี้คุณสามารถใช้สี, ปากกาเมจิก, ดินสอ, สีพาสเทล คุณสามารถติดด้ายกับรูปที่ทำเสร็จแล้วเพื่อให้สามารถแขวนได้ งานกระดาษประเภทนี้มักใช้เป็นของตกแต่งต้นคริสต์มาสในช่วงปีใหม่
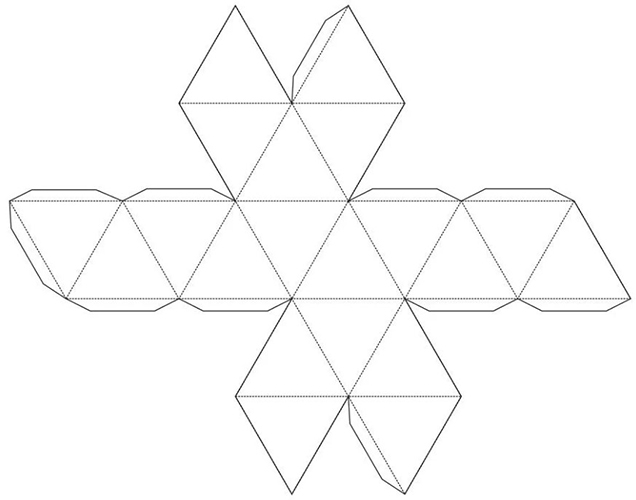
การใช้รูปทรงยี่สิบหน้าสามารถแตกต่างกันได้ มันไม่เพียงแต่ทำหน้าที่ด้านสุนทรียศาสตร์เท่านั้น แต่ยังทำหน้าที่เชิงปฏิบัติได้อีกด้วย
ทรงยี่สิบหน้าหลากสี
รูปแบบทรงยี่สิบหน้า (รูปแบบการติดกาวสามารถระบายสีได้) ที่มีหลายสีสามารถเป็นสื่อการเรียนรู้ด้านภาพที่ดีได้เมื่อต้องศึกษาเฉดสีกับเด็กเล็กที่สุด
ในการสร้างรูปทรงยี่สิบหน้าหลากสี คุณจะต้องมีวัสดุและเครื่องมือดังต่อไปนี้:
- เทมเพลตสำเร็จรูป(สามารถหาได้ง่ายบนอินเทอร์เน็ต)
- กระดาษสี (ถ้าไม่มี คุณสามารถระบายสีกระดาษสีขาวด้วยปากกาเมจิก สีหรือดินสอ ซึ่งจะน่าสนใจและสนุกสนานสำหรับเด็กๆ)
- กาว (แนะนำให้ใช้ PVA แห้งนาน)
- กรรไกร.
เมื่อเตรียมทุกอย่างเรียบร้อยแล้ว คุณสามารถดำเนินการสู่กระบวนการสร้างได้โดยตรง ซึ่งประกอบด้วยขั้นตอนต่างๆ ดังต่อไปนี้:
- สร้างช่องว่างโดยใช้สเตนซิล ส่วนจำนวนสีที่แตกต่างกันนั้น อาจใช้สีใดก็ได้ ขึ้นอยู่กับดุลพินิจของผู้ที่ประดิษฐ์งานนั้นๆ อย่างไรก็ตาม ยิ่งมีสีสันสดใสหลากหลายมากเท่าใด เด็กๆ ก็จะยิ่งชอบผลิตภัณฑ์นี้มากขึ้นเท่านั้น คุณสามารถใช้สีหลักของสายรุ้งเป็นตัวอย่างได้ คุณสามารถเพิ่มสีอีกสองสามสีหรือตรงกันข้ามก็ลบสีที่ดูไม่จำเป็นออกได้ (เช่น ไม่จำเป็นที่รูปหนึ่งจะต้องมีทั้งสีน้ำเงินและสีฟ้าอ่อน)
- เชื่อมต่อองค์ประกอบทั้งหมดโดยใช้กาว PVA แห้งยาวนาน
ทรงยี่สิบหน้ารูปดาว
รูปร่างทรงยี่สิบหน้าแบบดาวเป็นหนึ่งในรูปทรงที่ทำได้ยากที่สุด อย่างไรก็ตาม ความยากทั้งหมดอยู่ที่การที่คุณต้องมีความอดทนมาก งานนี้คงจะกินเวลานานมาก
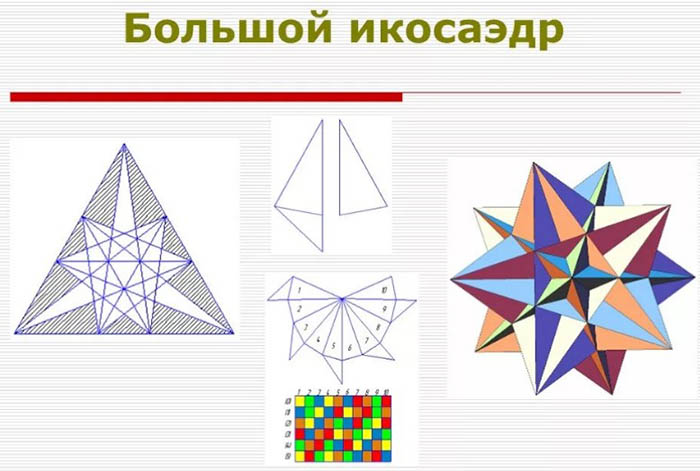
นอกจากความอดทนแล้ว คุณยังต้อง:
- กรรไกร;
- กระดาษสี;
- กาว.
คุณสามารถเตรียมองค์ประกอบตกแต่งบางส่วนเพื่อตกแต่งผลิตภัณฑ์สำเร็จรูปได้ สิ่งเหล่านี้อาจเป็นวัตถุใดๆ ก็ได้ที่ดูสวยงาม เช่น ด้ายหลากสี ริบบิ้น ลูกปัดติดกาว
เมื่อเตรียมทุกสิ่งที่จำเป็นเรียบร้อยแล้ว คุณสามารถดำเนินการสู่กระบวนการสร้างสรรค์ได้โดยตรง ซึ่งประกอบด้วยขั้นตอนต่างๆ ดังต่อไปนี้:
- ตัดกระดาษเป็นสี่เหลี่ยมจัตุรัส 30 ชิ้น โดยให้ด้านละ 5 ซม. แต่ละตารางเมตรจะต้องมีพื้นที่ 25 ตารางฟุต ดู. ในกรณีนี้คุณควรใช้กระดาษ 3 สี อาจเป็นโทนสีใดก็ได้ เช่น เขียว น้ำเงิน และแดง สุดท้ายควรจะมี 10 ช่องสำหรับแต่ละสี
- เมื่อตัดสี่เหลี่ยมตามจำนวนที่ต้องการแล้ว คุณสามารถหยิบชิ้นหนึ่งมาพับครึ่งหนึ่งได้ จากนั้นต้องพับครึ่งแต่ละด้านไปทางตรงกลาง แล้วยืดให้ตรง และพับมุมตรงข้ามสองครั้ง
- ทำให้แผ่นกระดาษดูเหมือนติ๊กแบบคลาสสิกซึ่งมักทำจากกระดาษ เมื่อต้องการทำเช่นนี้ ให้พับมุมใหญ่จากด้านล่าง
- จับด้านอื่นของสี่เหลี่ยม ควรพลิกกลับแล้วพับส่วนบนให้เป็นซอง ในกรณีนี้จะต้องใส่มุมแหลมเข้าไปในผลิตภัณฑ์
- ทำงานต่อด้วยสี่เหลี่ยมแรก ตอนนี้เมื่อมันกลายเป็นซองจดหมายแล้ว คุณต้องพับมันครึ่งหนึ่งและพับหูที่ยื่นออกมาโดยนำไปที่มุมด้านนอกของสามเหลี่ยม ขั้นตอนต่อไปหลังจากการยืดตรงก็จะสร้างหน่วยประกอบขึ้นมา
- เพื่อทำส่วนที่ใช้เวลานานที่สุดของงาน ควรทำซ้ำขั้นตอนทั้ง 5 ขั้นตอนที่อธิบายไว้ข้างต้นกับช่องที่เหลืออีก 29 ช่อง สิ่งนี้จะต้องใช้ความอดทนเป็นอย่างมาก อาจไม่สามารถสร้างโมเดลที่ต้องการทั้ง 30 โมเดลได้ในครั้งเดียว ขอแนะนำให้พักจากกระบวนการสร้างสรรค์นี้บ้าง
- เมื่อครบทั้ง 30 ชิ้นแล้ว คุณสามารถหยิบชิ้นส่วนหนึ่งและสอดปลายเข้าไปในช่องของชิ้นส่วนอื่นได้ (จำเป็นต้องมีสีที่แตกต่างกัน) ดังนั้นมุมขององค์ประกอบนี้จึงควรพอดีกับช่องของส่วนที่สามซึ่งมีสีแตกต่างจากอีกสองส่วน มุมชิ้นที่ 3 ควรพอดีกับช่องของชิ้นที่ 4 ซึ่งจะมีสีเดียวกับชิ้นที่ 1 วิธีนี้สีจะสลับกัน
- เสียบปลายชิ้นที่ 3 เข้าไปในชิ้นที่ 2 โดยใส่ชิ้นส่วนแรกเข้าไป และเอาปลายชิ้นส่วนที่สองออกให้เข้าไปในช่องของข้อต่อแรก
- ใส่ปริศนาที่ 2 เข้าไปในปริศนาที่ 3 จากนั้นใส่ปริศนาที่ 1 ลงไปในปริศนานั้น และปิดทั้งหมดด้วยปริศนาที่ 3
- ประกอบองค์ประกอบทั้งหมดตามแผนภาพด้านบน เมื่อองค์ประกอบสุดท้ายเข้าที่แล้ว งานอันยาวนานและยากลำบากในการสร้างรูปทรงยี่สิบหน้าแบบดาวก็ถือว่าเสร็จสิ้นแล้ว
ทรงยี่สิบหน้าประดับตกแต่ง
ตัวหนังสือเรขาคณิต 20 เหลี่ยมที่ทำจากกระดาษโดยใช้เทคนิคคุสุดามะนี้จะดูดีมากบนต้นคริสต์มาสในคืนส่งท้ายปีเก่า ในการสร้างรูปทรงยี่สิบหน้าแบบตกแต่ง คุณต้องตัดกระดาษเป็นสี่เหลี่ยมจัตุรัส 30 อัน ถ้าเป็นสีเหลืองอ่อนจะดีที่สุด

เมื่อเตรียมกระดาษสี่เหลี่ยมตามจำนวนที่ต้องการแล้ว คุณก็เริ่มกระบวนการสร้างสรรค์ได้:
- หยิบรูปสี่เหลี่ยมจัตุรัสอันหนึ่ง (เป็นรูปสี่เหลี่ยมจัตุรัสเท่ากันหมด คุณจึงหยิบอันไหนก็ได้) พับครึ่งหนึ่ง และพับด้านข้างมาไว้ตรงกลาง
จากนั้นจึงกางชิ้นงานและพับตามแนวเส้นกึ่งกลาง ต้องพับขอบเข้าหากึ่งกลางแล้วเปิดออกอีกครั้ง - งอชิ้นงานเพื่อให้รูปสี่เหลี่ยมกลายเป็นรูปสามเหลี่ยม หลังจากนั้นจะต้องยืดให้ตรงและดัดส่วนด้านข้างเข้าหาเส้นกึ่งกลาง จากนั้นพับขอบด้านล่างด้านหนึ่งไปด้านข้าง ผลลัพธ์จะต้องออกมาเป็นมุม ต้องพับขอบตรงข้ามเข้าหากึ่งกลางเพื่อให้เกิดจมูกแหลม
- ทำซ้ำขั้นตอนข้างต้นทั้งหมดอีกครั้ง แต่ตอนนี้ให้ทำกับด้านที่ 2 ของชิ้นส่วนด้วย ผลลัพธ์ที่ได้คือรูปสี่เหลี่ยมจัตุรัสที่มีปลายกรวยรูปสามเหลี่ยมสองอัน
- ต้องพับปริศนาตามยาว โดยพับรูปสามเหลี่ยมด้านเท่าด้านหนึ่งไปข้างหน้า และพับอีกด้านไปในทิศทางตรงข้าม
ขั้นตอนต่อไปคือการทำให้ชิ้นส่วนตรง ในการทำเช่นนี้คุณต้องดึงปลายของมัน นี้จะสร้างลิงก์แรกของรูปทรงยี่สิบหน้าตกแต่ง อย่างไรก็ตาม ควรมีลิงก์ทั้งหมด 30 ลิงก์ ดังนั้นจึงต้องดำเนินการอีก 29 ครั้ง - เมื่อองค์ประกอบทั้ง 30 ชิ้นพร้อมแล้ว คุณสามารถเริ่มเชื่อมต่อพวกมันได้ ทำได้ดังนี้คือ ปลายของลิงก์อันหนึ่งจะต้องสอดเข้าไปในช่องของลิงก์อีกอันหนึ่ง จากนั้นปลายของข้อที่ 3 จะถูกสอดเข้าไปในช่องเดียวกัน และปลายของตัวที่ 4 สอดผ่านตัวที่ 5 จากนั้นแทรกตัวที่ 1 เข้าไปในตัวที่ 5 ทำให้เกิดวงแหวนปิด
- ส่วนปลายกลีบดอกถัดไปทั้งหมดต้องวางไว้ในช่องว่างระหว่างข้อเพื่อให้เป็นรูปสามเหลี่ยม
- แต่ละส่วนจะต้องผ่านขั้นตอนที่คล้ายคลึงกัน หลังจากปิดสามเหลี่ยมสุดท้ายแล้ว จะได้รูปร่างสวยงามที่จะดูสวยงามบนต้นคริสต์มาส
เมื่อเข้าใจวิธีการสร้างลวดลายกระดาษเพื่อติดกาวรูปทรงยี่สิบหน้าแล้ว คุณก็สามารถเริ่มสร้างแบบจำลองด้วยตัวเองได้โดยใช้สี วัสดุ และการตกแต่งที่หลากหลาย
วิดีโอเกี่ยวกับการทำรูปทรงยี่สิบหน้าด้วยกระดาษ
มาสเตอร์คลาสเกี่ยวกับการสร้าง icosahedron ที่มีรู:
